最近のマイブーム
最近、SFCのすーぱーぷよぷよ通Remixにハマってます。今更ながら、ですが(笑)。
さて、これ遊びながら思ったんですが、あまりにもぷよの出現が偏りがあって、
「あんま良い乱数使ってないんじゃないの?」
とかぶつくさボヤいてたんですが(笑)。
しかし待てよ、と。どういう風に乱数プログラミングしてたんだろ?
※ もっとも、良い乱数使ったから、と言って、このテの落ち物パズルのゲーム性が上がる、とは限らないんですがね(笑)。
機械語には乱数は無い
ここんとこ、色々古いCPU、例えば6502とかZ80の資料を眺めていたんですが。
基本的には(当たり前かもしれないですが)機械語では「擬似乱数列」ってのは用意されてないんですね。
スーファミのCPUは65816と言うApple II GSで使用されていた、あまりメジャーじゃないCPUが使われています。
90年代初頭のスーファミの時代、ゲームプログラマはアセンブリ言語でプログラムする事が多かった模様です。そして当時は(ある程度は用意されてたみたいですが)開発ツールなんてのも今のようにゴージャスじゃなかった模様です。
と言う事は、かなりの確率で、例えばアクションゲームとかシューティングならさておき、RPG等、自作のアセンブリで書いた乱数ライブラリを使ってたりしたんじゃないでしょうか。そうじゃないと16bit CPU程度ではスピードはあんま稼げなかった筈なんですよね。
擬似乱数。果たしてどうやってプログラムするんでしょう。
SICPの乱数
話は唐突に飛びますが。
計算機プログラムの構造と解釈でも中途半端に(笑)、擬似乱数の作り方が載っています。
「ランダムに選ばれた」の意味は明瞭ではない. おそらく望んでいるのは randの次々の呼び出しは一様分布という統計の性質を持つ数列を生成することである. 適切な数列の発生法はここでは論じない. そうではなく, 手続きrand-updateがあり, ある数x1から出発し,
x2 = (rand-update x1)x3 = (rand-update x2)
を作ると, 値の列x1, x2, x3, ... は望みの統計的性質を持つと仮定する.
randをある固定した値random-initに初期化される局所状態変数xを持った手続きとして実装出来る. randを呼び出す度にxの現在値のrand-updateを計算し, これを乱数として返し, またそれをxの新しい値とする.
(define rand (let ((x random-init)) (lambda () (set! x (rand-update x)) x)))
もちろん同じ乱数の列を単にrand-updateを直接呼び出すことで, 代入なしに生成することが出来る. しかしプログラムの乱数を使う部分は rand-updateに引数として渡すxの値をしっかり覚えていなければならないことを意味する.
そして注釈には次のような記述があります。
要するに具体的な例は全く紹介されてないんですね(笑)。
そこでWikipediaを頼ったコードは次のようなモノです。
これは線形合同法と言う極めて単純なやり方なんですが。ところが精度がメチャクチャ悪いんですね。
SICPではこの後、円周率πをモンテカルロ・シミュレーションで求めよう、ってトピックになるわけですが。
ところが、これやってみりゃ分かるんですが、円周率πに届かないんですよ(笑)。
さては、この結果知ってて「乱数作成」をサラーっと流したんじゃねぇの(笑)。
もう、SICP、こんなんばっかだよ(苦笑)。
実はSchemeって仕様には乱数が含まれてないんですね。
まあ、もちろん、各実装には実装依存で乱数生成プログラムが入ってるんでしょうが、あくまで「仕様としては」乱数は持ってません。
そう言う意味では結構メンドくせぇプログラミング言語なんですよね(笑)。
一方Lispはどうか、と言うと例えば、Common Lispなんかにはメルセンヌ・ツイスタのライブラリが公開されていて、共有されています。
Schemeは・・・・・・まあ、実装次第なんでしょうねぇ。Gaucheなんかはメルセンヌ・ツイスタを使ってたと思うんですが、他の実装だと保証の限りじゃないです。まあ、こう言う時、「ライブラリを共有しづらい」Schemeだとやりにくいですね(R7RSでだいぶ仕様上は改善されていますが)。
さて、Racketはどうでしょうか?
何だそりゃ。初めて聞きました。
実はCのソースコードが公開されていました。
これって結構シンプルじゃね?
さぁ、やっと本題です(笑)。
今回はこのMRG32k3aと言うアルゴリズムをRacketで「遅延評価を使って」実装してみたいと思います。SICPの遅延評価の乱数ストリームの仇をここで取ります(笑)。
Schemeでは仕様上、遅延評価に絡んだ機能はdelayとforceしか提供していません。
これだけだと甚だメンド臭く、「マトモに遅延評価をさせる」には、色々基本的な遅延評価用の手続きを実装しないといけません。事実、SICPの遅延評価の項目だとそこに結構な量が割かれているんですよね。
それじゃああんまりにもメンドくせえだろ、って言う貴方に朗報です(笑)。
実は分かりづらいんですが、SRFI-41ってのがあって、これを呼び出せば遅延評価の基本機構は使い放題、となります。
主なトコではstream-cons、stream-car、stream-cdr、stream-null、stream-map、stream-filter、stream-constant、stream-ref、stream-from等等等、SICP程度のお題ならこの程度で大体書けるようになってるライブラリです。
便利でこの辺考えなくって良いんで、これを使いましょう。
まずは大域変数をCコードに則って定義していきます。まあ、最終的にはこれらはletで局所変数化されるんですが、最初はまあ、Cのコードそのままで書いていきます。
さすがC、Lisp慣れしてると物凄くゴチャゴチャして見えますが(笑)。
原因の一つってのはここの箇所って実は「2つの事柄が1つにまとまってる」からなんですよね。
ここで行われてるのは次の2つです。
そしてp1を計算するComponent1なるプロシージャを設計すれば良い。オリジナルのCコードだと次の部分ですね。
ちなみに、最初、この2行目と3行目で何やってんだかサッパリ分かんなかったんですけど、何とこれ剰余計算やってるみたいです(笑)。え"え"え"え"え"、とか思ったんですが(苦笑)。うげぇ(笑)。
何で%使わねぇのかな。不思議です。ま、いいや(苦笑)。
つまり、この部分をSchemeで書くとこうなる、って事ですね。
stream1とComponent1を組み合わせると、例えば実行結果は次のようになります。
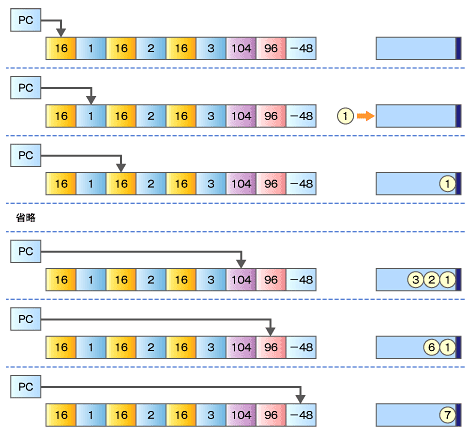
stream1の最初と2番目と3番目の値はSEEDの値、4番目、5番目の値はそれぞれ1番目と2番目、2番目と3番目の値を使って計算してるから同じ値、6番目からガラッと変わってきますね。
これはstream->listと言うプロシージャでアタマ10個分だけ「実体化」させたわけですが、これがずーっと「無限ストリーム」として続いていくわけです。
ただしComponent1とは使ってる引数の値と引数の順番が若干違うんで引っかからないように(笑)。
この辺をstream-mapを使って上手いこと実装します。
Combinationは新しいストリーム、ここでは乱数列を返します。
ちょっとまた、アタマ10個くらいstream->listで実体化させて見てみます。
おお、上手く動いてるようですね。
例えば乱数列の100番目、1000番目、10000番目はそれぞれ
となります。
おお、面白い(笑)。これで(基本的に)実装は完了です。
rand-updateを実装する通常のやり方は, a, b, mを適切に選んだ整数とし, mを法としてxをax + bで更新する規則を使うことである.
要するに具体的な例は全く紹介されてないんですね(笑)。
そこでWikipediaを頼ったコードは次のようなモノです。
これは線形合同法と言う極めて単純なやり方なんですが。ところが精度がメチャクチャ悪いんですね。
SICPではこの後、円周率πをモンテカルロ・シミュレーションで求めよう、ってトピックになるわけですが。
ところが、これやってみりゃ分かるんですが、円周率πに届かないんですよ(笑)。
さては、この結果知ってて「乱数作成」をサラーっと流したんじゃねぇの(笑)。
もう、SICP、こんなんばっかだよ(苦笑)。
Schemeと乱数
ところで。実はSchemeって仕様には乱数が含まれてないんですね。
まあ、もちろん、各実装には実装依存で乱数生成プログラムが入ってるんでしょうが、あくまで「仕様としては」乱数は持ってません。
そう言う意味では結構メンドくせぇプログラミング言語なんですよね(笑)。
最強の乱数生成法
統計処理言語Rやお馴染みのPythonではメルセンヌ・ツイスタと言われる乱数生成プログラムが組み込まれています。メルセンヌ・ツイスタは今のトコ、史上最強と言われる擬似乱数生成プログラムで、仕様がない言語で最強の乱数列が使い放題なんですよねぇ。一方Lispはどうか、と言うと例えば、Common Lispなんかにはメルセンヌ・ツイスタのライブラリが公開されていて、共有されています。
Schemeは・・・・・・まあ、実装次第なんでしょうねぇ。Gaucheなんかはメルセンヌ・ツイスタを使ってたと思うんですが、他の実装だと保証の限りじゃないです。まあ、こう言う時、「ライブラリを共有しづらい」Schemeだとやりにくいですね(R7RSでだいぶ仕様上は改善されていますが)。
さて、Racketはどうでしょうか?
Racketの乱数
残念ながらRacketの乱数はメルセンヌ・ツイスタではございません(笑)。RacketのDocumentationによると、L’Ecuyer’s MRG32k3a algorithmと言うアルゴリズムを用いてるそうです。何だそりゃ。初めて聞きました。
実はCのソースコードが公開されていました。
これって結構シンプルじゃね?
さぁ、やっと本題です(笑)。
今回はこのMRG32k3aと言うアルゴリズムをRacketで「遅延評価を使って」実装してみたいと思います。SICPの遅延評価の乱数ストリームの仇をここで取ります(笑)。
遅延評価の友
ところで。Schemeでは仕様上、遅延評価に絡んだ機能はdelayとforceしか提供していません。
これだけだと甚だメンド臭く、「マトモに遅延評価をさせる」には、色々基本的な遅延評価用の手続きを実装しないといけません。事実、SICPの遅延評価の項目だとそこに結構な量が割かれているんですよね。
それじゃああんまりにもメンドくせえだろ、って言う貴方に朗報です(笑)。
実は分かりづらいんですが、SRFI-41ってのがあって、これを呼び出せば遅延評価の基本機構は使い放題、となります。
主なトコではstream-cons、stream-car、stream-cdr、stream-null、stream-map、stream-filter、stream-constant、stream-ref、stream-from等等等、SICP程度のお題ならこの程度で大体書けるようになってるライブラリです。
便利でこの辺考えなくって良いんで、これを使いましょう。
※ 何故SRFI-41が「分かりづらい」かと言うと、遅延評価、つまりlazy-evaluationとして題名が付いてなくって「stream」と言う分かりづらい用語になってるからに他ならない。これは歴史的要因で、今ではlazy-evaluationと言う呼び方の方が妥当になってるが、過去にはそのままstreamと呼ばれてた事に由来する。
実装方針
最終的には単一のプロシージャにまとめますが、途中までは色々バラバラのパーツとして組み立てて行こうと思います。じゃないと遅延評価って良くわかりませんからね。大域変数
まずは大域変数をCコードに則って定義していきます。まあ、最終的にはこれらはletで局所変数化されるんですが、最初はまあ、Cのコードそのままで書いていきます。
この辺はまあ、いいですよね。乱数の種、SEEDも12345と言うフザけた(笑)値が与えられています。
ちなみに、実はm1、m2と言う2つの値は2の32乗から下2つの素数の模様です。
ちなみに、実はm1、m2と言う2つの値は2の32乗から下2つの素数の模様です。
Component
さて、Cソースのコメントで、取り敢えずComponent 1と書かれたところに着目してみます。さすがC、Lisp慣れしてると物凄くゴチャゴチャして見えますが(笑)。
原因の一つってのはここの箇所って実は「2つの事柄が1つにまとまってる」からなんですよね。
ここで行われてるのは次の2つです。
- p1 なる値の計算
- s10、s11、s12と言う3つの数の更新
当然Lisperとしては(笑)、「2つの計算目的は2つのプロシージャで書くべきだ」と言う原則を守ろうと思います。
さて、では手始めに2番から行きますか。
実はさっき定義しなかったんですが、原版ではs10、s11、s12と言う3つの値も大域変数として定義されています。
しかし「遅延評価を持ったLisp」であるSchemeではこれはやるべきじゃないトコなんですよね。
つまり、「各値を更新する」んじゃなくって、s10、s11、s12、そしてその後にはs13、s14・・・って「続いていくだろう」無限ストリームがある、って考えた方がスマートなわけです。
実際は、元のCコードを見ると、
(SEED SEED SEED p1 ....)
と言うようなカタチの無限ストリームを想定出来そうだ、って事ですよね。そしてp1以降は適当なプロシージャ、具体的には1の「計算によって」得られた数値がハマっていく。
そう言う想定から言うとまずは次のような「ストリーム生成」プロシージャをでっち上げられます。
そしてp1を計算するComponent1なるプロシージャを設計すれば良い。オリジナルのCコードだと次の部分ですね。
ちなみに、最初、この2行目と3行目で何やってんだかサッパリ分かんなかったんですけど、何とこれ剰余計算やってるみたいです(笑)。え"え"え"え"え"、とか思ったんですが(苦笑)。うげぇ(笑)。
何で%使わねぇのかな。不思議です。ま、いいや(苦笑)。
つまり、この部分をSchemeで書くとこうなる、って事ですね。
stream1とComponent1を組み合わせると、例えば実行結果は次のようになります。
stream1の最初と2番目と3番目の値はSEEDの値、4番目、5番目の値はそれぞれ1番目と2番目、2番目と3番目の値を使って計算してるから同じ値、6番目からガラッと変わってきますね。
これはstream->listと言うプロシージャでアタマ10個分だけ「実体化」させたわけですが、これがずーっと「無限ストリーム」として続いていくわけです。
Component2
基本ロジックはComponent1と全く同じなんでサクッと書いていきます。ただしComponent1とは使ってる引数の値と引数の順番が若干違うんで引っかからないように(笑)。
Combination
現時点ストリームが2つあります。p1、p2はそれぞれのストリームの4番目からスタートして、条件に従ってどっちかを選択してちょこちょこと計算して新しいストリームに組み込まれるわけです。この辺をstream-mapを使って上手いこと実装します。
Combinationは新しいストリーム、ここでは乱数列を返します。
ちょっとまた、アタマ10個くらいstream->listで実体化させて見てみます。
おお、上手く動いてるようですね。
例えば乱数列の100番目、1000番目、10000番目はそれぞれ
となります。
おお、面白い(笑)。これで(基本的に)実装は完了です。