Schemeでスタックマシンの基礎

Wizardryってゲームが好きです。

まあ、あまりにも有名なゲームなんで知らない人は多分いないと思うんですが、一応ちょっと解説してみますか。
世界で初めて、商用として成功したRPG(ロールプレイングゲーム)ですね。

注: 良く「世界初のRPG」って記述が成されますが、これは嘘です。実は世界初のRPGはPLATOと言うメインフレームのプラットフォームで作られていて、それは1974年頃の事でした。WizardryはそのPLATOで1977年頃に作られたMMORPG(ビックリするかもしれないけど、ネット時代より遥か以前にMMORPGは既に存在していた!)であるOublietteと言うゲームをApple II上で1人でプレイできるように「改良した」もの、って言って良いです。

さて、このWizardryってのは色々なマシンに移植されてるわけですが。ファミコンみたいなゲーム専用機以外でもザーッと挙げてみると、

• Apple II
• Apple Macintosh
• SHARP MZ-2500
• SHARP X1/Turbo
• 富士通 FM-7
• 富士通 FM-77
• NEC PC-8801
• NEC PC-9801
• MSX-2
• Commodore 64
• Commodore 128
• IBM-PC

と物凄い数の移植なんですね。

これだと物凄い数のプログラマが物凄く苦労して移植したんじゃないか、って思うでしょう。ところが、メインプログラマのロバート・ウッドヘッド氏の話によると、

「殆ど(80%くらい?)ソースコードは同じなんだ。違うのは画像出力とか、機械によって差があるところだけだね。」

との事です。

当時のゲームプログラムだとBASIC、あるいはスピードが欲しい場合は直接アセンブリでコーディングするのが普通だったらしいんですが、Wizardryの設計の優れたところ、と言うのは、Pascalを使った構造化プログラミングで作ったほぼ最初の商用製品だ、と言うトコロでしょう。完全にシナリオデータとゲーム本体のプログラムを分けているらしく、外国語へのポーティングも必要最小限の労力で行えるように設計されているらしく、恐らく凄く綺麗な「教科書的な」プログラミングの塊なんじゃないでしょうか。

ここで使われたPascal処理系をUCSD Pascalと言います。これは仮想マシン上で動くように設計されたPascal処理系の代表格で、まさに当時の"Write Once, Run Anywhere"を実現してたようですね・・・そう、当時はJava的な存在だったわけです。

注: C言語も「マシン間の差異があってもソースの移植性を極力大事にする」意図で設計されていますが、随分と違うアプローチで、元々Pascalは「仮想マシンを前提として動かす」と言うアプローチになってました。しかも、C言語は原則的に16bit機以上が対象で、黎明期の8bitのパーソナルコンピュータ上だと「動かしづらい」プログラミング言語だった模様です。その辺、当時の環境だとPascalの方がメリットが大きかったのでしょう。

 さて、そのUCSD Pascal。Wikipediaではこんな記述が成されていますね。

CPUの異なるパーソナルコンピュータ上で動作するために、P-Machineと呼ばれる仮想マシンを使用する。コンパイラはプログラムをそれぞれのCPU用の機械語に翻訳するのではなく、P-Machineの機械語であるP-Codeに翻訳する。そのため、P-Codeの仮想マシンを実装すればどのようなパーソナルコンピュータ上でも実行可能であった。

かっちょいい(笑)!仮想マシンですよ、仮想マシン(笑)。
問題は仮想マシンってのは実装が簡単なんですかねぇ。次のような記述が続きます。

 P-Machineは典型的なスタックマシンで、様々な処理を主にスタック上で行うアーキテクチャを持っていた。

スタックマシン・・・何じゃそれ、なんですが(笑)。
Wikipediaのスタックマシンの項目読んでてもイマイチピンと来ない。 やっぱ一回実装してみるに限りますね。
元々、CPUの動作とかは全く知らない門外漢なんですが、そろそろその辺勉強しても良い頃かもしれません。
ってなわけで、ネットで検索するとJavaで書かれた「仮想計算機を作ろう」と言うページを見つけたんで、Java書けないんですが(笑)、何とか読み下して、Schemeで簡単なスタックマシンを実装してみたいと思います。

スタックとは何か?

知るか(笑)。

いや、昔勉強した事あった、って言えばあったんですが、「一体何の為にこれやってんのか」ってのがサッパリ分からないんで、すっかり忘れてます(笑)。Lisp系だと何でもリストを使えば済む、ってんであんまマジメに考えてなかったんですよねぇ。改めて勉強です。

仮想スタックマシンを実装するに当たって、スタックというデータ構造について理解している必要がありますから、まずはこれについて、簡単なプログラムを交えながら解説することにします。

はいはい。

スタックはデータ構造の1つで、LIFO（Last In First Out）という性質を持っています。これは、最後に入れたデータを最初に取り出すことができるという意味になります。

何か、んな事言ってたなぁ。

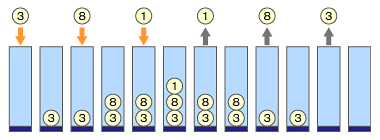
ボール（値）を上からしか出し入れできない、不透明な長い箱をイメージするとよいでしょう。このような箱からボールを取り出すには、最後に入れたボール（値）からしか取り出せないということになります。

 値をスタックへ格納する操作はpushと呼ばれ、値をスタックから取り出す操作はpopと呼ばれます。この2つの基本操作でスタックへ格納するデータをコントロールできます。オレンジ矢印が値を積むpushの操作を表し、グレイ矢印が値を取り出すpopの操作を表しています。次に取り出せるデータを参照するためのpeekという操作が提供されることもあります。

 スタックにはどのような値がどういう順番で格納されているのかについては隠ぺいされていて、スタックを使用するプログラムからは見えないという点も重要です。

 このように、スタックでは単純な操作しかできないのですが、後置記法と組み合わせることにより結構複雑な計算を実現できます。基本動作を理解するために、スタックの使い方と簡単な実装方法について見てみましょう。

なるほど、です。
次へ進んでみましょうか。

スタックを実装してみる

まずは、そのpushとpopを実装してみます。 Schemeだと次のように実装するのが綺麗なんじゃないでしょうか。

	(define (push item stack)
	(cons item stack))
	(define (pop stack)
	(values (car stack) (cdr stack)))

view raw push and pop.rkt hosted with ❤ by GitHub

pushは事実上consですね。ここは良し、とします。
問題はpopですか。通常、恐らく大域変数stackをリストで作っておいて、破壊的変更を行う、ってのがこのテのコーディングの前提になるんでしょうが、それは避けます。あくまで関数型プログラミングの範疇で、破壊的変更しない前提で行きます。
が、そうすると困ったことになるんですね。原則、pushではstackは仮引数として与えてstackに何らかの操作をした結果を返せばいいわけですが、popの場合、「取り出した値を返す」のが大事なのか「操作した後のstackを返す」のが大事なのか分かりません。ってかどっちも大事なんですよね～。
こう言う場合多値を用いて両者とも返しちゃう、ってのが一番Schemeらしいでしょう。そう言う実装方針で上のコードは掻きました。

次に示すような順番でスタックへ値を積んだり、スタックから値を取り出したりしてみます。

 ここでは、図2のボール1をItem1、ボール2をItem2のように表すことにします。図2の動作例に従い、Item1、Item2、Item3の値を順にスタックへ積んだ（push）後、スタックから値を取り出します（pop）。このとき、一番上にある値はItem3なので、これが取り出されます。

 次に、Item4、Item5の値を順にスタックへ積んでから、3回連続でスタックから値を取り出します。このとき、スタックの上から順に値が取り出されるので、Item5、Item4、Item2の順に出てきます。このタイミングでは、スタックにはItem1しか残っていないということになります。

 最後に、ここへItem6を積んで、2回連続でスタックから値を取り出します。すると、Item6、Item1の順で値が取り出されます。

では、ここで書いてあるような動作をテストするプロシージャ、stacktestを実装してみます。こう言う場合、Schemeだとちょっと汚くなる、っつーかSchemeらしい書き方が難しいんですよね。何せ逐次実行が前提の言語じゃないんで、フラットに書くのが難しい。
一方、所詮動作確認なんで、あんま面倒臭い事考えたくないんで、適当にベタ書きしてみます。

	(define (stacktest . stack)
	(let ((stack (push "Item1" stack)))
	(let ((stack (push "Item2" stack)))
	(let ((stack (push "Item3" stack)))
	(let-values (((item stack) (pop stack)))
	(display item) ; Item3
	(newline)
	(let ((stack (push "Item4" stack)))
	(let ((stack (push "Item5" stack)))
	(let-values (((item stack) (pop stack)))
	(display item) ; Item5
	(newline)
	(let-values (((item stack) (pop stack)))
	(display item) ; Item4
	(newline)
	(let-values (((item stack) (pop stack)))
	(display item) ; Item2
	(newline)
	(let ((stack (push "Item6" stack)))
	(let-values (((item stack) (pop stack)))
	(display item) ; Item6
	(newline)
	(let-values (((item stack) (pop stack)))
	(display item) ; Item1
	(newline)
	stack)))))))))))))

view raw stacktest.rkt hosted with ❤ by GitHub

オリジナルのJavaコードに対応させようとすると、大体こんなカンジですかね。Javaなんかは由緒正しい「逐次処理言語」なんで、コードがフラットなんですが、Schemeの場合、特に今回はpopが多値を返す為にこう言うヘンなカンジにならざるを得なかったです。
ポイントはlet-valuesで、popが多値を返し、最初の値(つまり取り出した値)を表示用のプロシージャ、displayに渡して表示させて、残りをstackとして次のプロシージャに渡すようになっています。

	(let-values (((item stack) (pop stack))) ; pop の2つの返り値を item と stack に束縛する
	(display item) ; item を表示
	(newline) ; 改行
	(hoge stack)... ; stack を別のプロシージャへ渡す

view raw let-values sample.rkt hosted with ❤ by GitHub

では動作確認してみましょうか。

	> (stacktest)
	Item3
	Item5
	Item4
	Item2
	Item6
	Item1
	'()
	>

view raw stacktest.rkt hosted with ❤ by GitHub

元ページのJavaコードの実行結果と同じになっていますね。確かにLIFOになっています。

仮想スタックマシンを実装する

すでに何度か説明しましたが、後置記法で表現された式というのは、スタックを使うと、非常に簡単に計算ができてしまいます。そして、このスタックというデータ構造を実現することは、これまでの説明からも分かるように、それほど難しくはありません。

さいでっか。じゃあ、次行きましょうか。

設計

オリジナルだとクラスだフィールドだメソッドだ、って書いてるんですが、Schemeにはんなモン無いんで無視します(笑)。そもそも大域変数を破壊的変更する設計にしないんで、フィールドとか要らんでしょ。

ただ、簡単化の為に次のヤツだけは受けます。

また、演算装置も用意します。これは、2つのパラメータを受け取って演算を行い、その結果を返すメソッドを持つAluクラスとして実装します。ALU（Arithmetic Logic Unit）は四則演算と論理演算を含むのが一般的ですが、ここではSvm1に必要な加算と乗算のみ用意することにします。

そうそう、面倒だから取り敢えず加算と乗算のみやることにしましょう。追加は簡単ですしね。

演算装置

まあ、これは簡単ですね。オリジナルだとメソッドにしてますが、Schemeでは単純に独立したプロシージャとして実装します。ってか実装って程でもねぇんだけどな。

	(define (add a b)
	(+ a b))
	(define (multiply a b)
	(* a b))

view raw alu.rkt hosted with ❤ by GitHub

まんまやん、まんま、そのまんまです。

プログラムを仮想スタックマシンへロード

さて、オリジナルではバイトデータのファイルでやり取りしてるんですが、どうしましょう。そもそもSchemeだとバイトデータの扱いが良く分からないし(そもそも仕様にないと思う)、オリジナルのバイトデータの仕様も良く分かりません。

しょーがないんで、プレーンテキストの読み込みに留めておきます。

そしてそのプレーンテキストへの記述の仕様ですが、

• 計算式は逆ポーランド記法とする
• bipush命令は続くコードにある値をオペランドスタックに積む(push)
• iadd命令はオペランドスタックに積まれている値を2つ取り出して(pop)、それぞれの値を加算した結果をオペランドスタックに積む
• imul命令はオペランドスタックに積まれている値を2つ取り出して(pop)、乗算した結果をオペランドスタックに積む
• print命令はオペランドスタックの一番上に積まれている値を出力する

とします。

具体的には、例えば、1 + 2 * 3の演算命令としては、基本的には逆ポーランド記法なので、1 2 3 * +になるわけですが、テキストファイルへの記述は

bipush 1 bipush 2 bipush 3 imul iadd print

view raw code1.svm hosted with ❤ by GitHub

とします。
何だかインチキなアセンブリ言語みたいですが(笑)、取り敢えずこれを良しとして対象としましょう。構造さえ決まってしまえば、あとでどうにでも改造出来ますしね。

ってなわけでloadプロシージャを決まりきったカタチで実装します。

	(define (load filename)
	(with-input-from-file filename
	(lambda ()
	(let loop ((code '()) (c (read)))
	(if (eof-object? c)
	(reverse code)
	(loop (cons c code) (read)))))))

view raw load.rkt hosted with ❤ by GitHub

ロードしたプログラムを実行

余談ですが、Schemeの最新の仕様書では繰り返し構文が増えています。他の言語ではお馴染みのwhen(while)やunlessが搭載されました。繰り返ししたいけど特に終了時点で返したい値が無い場合重宝しますね。

ってなわけでunlessを使った再帰でプロシージャexecuteを実装します。

	(define (execute code stack)
	(unless (null? code)
	(let-values (((code stack) (executecommand code stack)))
	(execute code stack))))

view raw execute.rkt hosted with ❤ by GitHub

executeはexecutecommandを呼び出し、executecommandは多値を使ってexecuteとの間でcodeとstackをやり取りします。codeはexecutecommandによって「消費」され、計算の進行に従ってstackは(プログラミング用語ではない)状態を変化させていきます。命令を実際に解釈していくのはexecutecommandです。
ではexecutecommandを実装していきます。

命令の判定を実行

• commandがbipushの場合は、続くコードにある値をオペランドスタックへ積む（push）する処理を行います。

• commandがiaddの場合は、オペランドスタックに積まれている値を2つ取り出して（pop）、それぞれの値を加算した結果をオペランドスタックへ積みます。

• commandがimulの場合は、iaddとほぼ同様の処理を行いますが、オペランドスタックへは取り出した値を乗算した結果を積むという点が異なります。

• commandがprintの場合は、オペランドスタックの一番上に積まれている値を出力します。

これをこのまま実装すると次のようになります。

	(define (executecommand code operandstack)
	(let ((command (car code)) (code (cdr code)))
	(case command
	((bipush) (values (cdr code) (push (car code) operandstack)))
	((iadd) (let-values (((b operandstack) (pop operandstack)))
	(let-values (((a operandstack) (pop operandstack)))
	(values code (push (add a b) operandstack)))))
	((imul) (let-values (((b operandstack) (pop operandstack)))
	(let-values (((a operandstack) (pop operandstack)))
	(values code (push (multiply a b) operandstack)))))
	((print) (display (peek operandstack))
	(newline)
	(values code operandstack)))))

view raw executecommand.rkt hosted with ❤ by GitHub

先ほど書いた通り、executecommandはexecuteと多値を用いてやり取りします。返り値はcodeとoperandstackの二種類です。

仮想計算機もどきの実行

例として、次の3つのファイルを用意しておきます。

bipush 1 bipush 2 iadd print

view raw code0.svm hosted with ❤ by GitHub

bipush 1 bipush 2 bipush 3 imul iadd print

view raw code1.svm hosted with ❤ by GitHub

bipush 1 bipush 2 iadd bipush 3 imul print

view raw code2.svm hosted with ❤ by GitHub

このプログラムで生成されたSvm1のオブジェクトコードを仮想スタックマシンSvm1で実行します。

では、svm1をでっち上げましょう。

	(define (svm1 filename)
	(execute (load filename) '()))

view raw svm1.rkt hosted with ❤ by GitHub

code0.svmには、「1 + 2」、code1.svmには、「1 + 2 * 3」、code2.svmには、「(1 + 2) * 3」を計算するオブジェクトコードが保存されていますから、実行結果はそれぞれ「3」、「7」、「9」となります。

	> (svm1 "./code0.svm")
	3
	> (svm1 "./code1.svm")
	7
	> (svm1 "./code2.svm")
	9
	>

view raw execute-svm1.rkt hosted with ❤ by GitHub

はい、確かになっていますね。

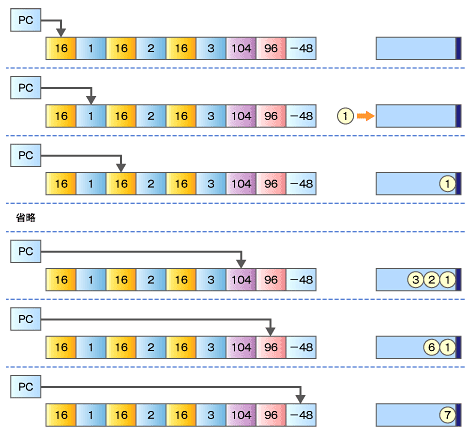
仮想計算機の実行例のイメージ

1. 最初に、bipushを読み込むと、次の値を読み込んでオペランドスタックへ「1」をpushしています。同様にして、「2」「3」をpushします（図では、省略しています）。
2. imulを読み込むと、オペランドスタックから値を2つpopして、それらを乗算し、その結果をオペランドスタックへpushします。
3. iaddを読み込むと、オペランドスタックから値を2つpopして、それらを加算し、その結果をオペランドスタックへpushします。

どうでしょう、スタックを使うと簡単に仮想計算機をソフトウェアで実装することが分かったでしょうか。もちろん、Svm1は仮想計算機というには機能が少な過ぎますが、雰囲気はつかんでいただけたと思います。

まあ、雰囲気はつかめましたね、確かに。

今回のソース

さあて、これ使うと色々な仮想計算機が作れる足がかりになるんでしょうかね。
では今回のソースです。

	#lang racket
	(define (push item stack)
	(cons item stack))
	(define (pop stack)
	(values (car stack) (cdr stack)))
	(define (peek stack)
	(car stack))
	(define (stacktest . stack)
	(let ((stack (push "Item1" stack)))
	(let ((stack (push "Item2" stack)))
	(let ((stack (push "Item3" stack)))
	(let-values (((item stack) (pop stack)))
	(display item) ; Item3
	(newline)
	(let ((stack (push "Item4" stack)))
	(let ((stack (push "Item5" stack)))
	(let-values (((item stack) (pop stack)))
	(display item) ; Item5
	(newline)
	(let-values (((item stack) (pop stack)))
	(display item) ; Item4
	(newline)
	(let-values (((item stack) (pop stack)))
	(display item) ; Item2
	(newline)
	(let ((stack (push "Item6" stack)))
	(let-values (((item stack) (pop stack)))
	(display item) ; Item6
	(newline)
	(let-values (((item stack) (pop stack)))
	(display item) ; Item1
	(newline)
	stack)))))))))))))
	(define (add a b)
	(+ a b))
	(define (multiply a b)
	(* a b))
	(define (load filename)
	(with-input-from-file filename
	(lambda ()
	(let loop ((code '()) (c (read)))
	(if (eof-object? c)
	(reverse code)
	(loop (cons c code) (read)))))))
	(define (execute code stack)
	(unless (null? code)
	(let-values (((code stack) (executecommand code stack)))
	(execute code stack))))
	(define (executecommand code operandstack)
	(let ((command (car code)) (code (cdr code)))
	(case command
	((bipush) (values (cdr code) (push (car code) operandstack)))
	((iadd) (let-values (((b operandstack) (pop operandstack)))
	(let-values (((a operandstack) (pop operandstack)))
	(values code (push (add a b) operandstack)))))
	((imul) (let-values (((b operandstack) (pop operandstack)))
	(let-values (((a operandstack) (pop operandstack)))
	(values code (push (multiply a b) operandstack)))))
	((print) (display (peek operandstack))
	(newline)
	(values code operandstack)))))
	(define (svm1 filename)
	(execute (load filename) '()))

view raw stackmachine.rkt hosted with ❤ by GitHub